Modeling
Department of Information Science
College of Computing and Informatics
Drexel University
Some themes
What is modeling?
The role of mathematics
Calculus
Differential calculus is about rates (slopes)
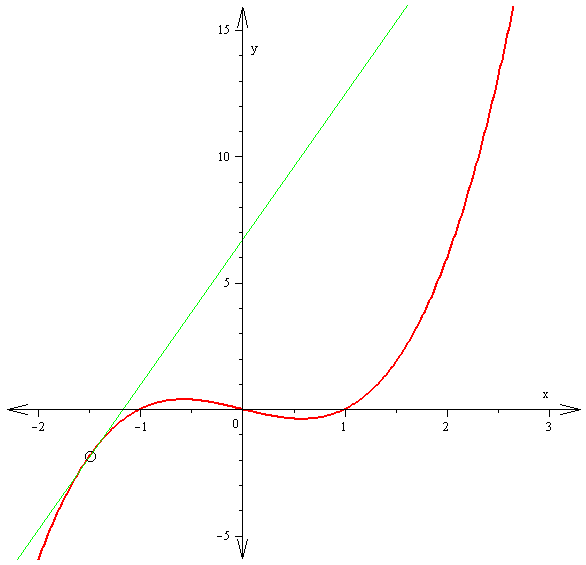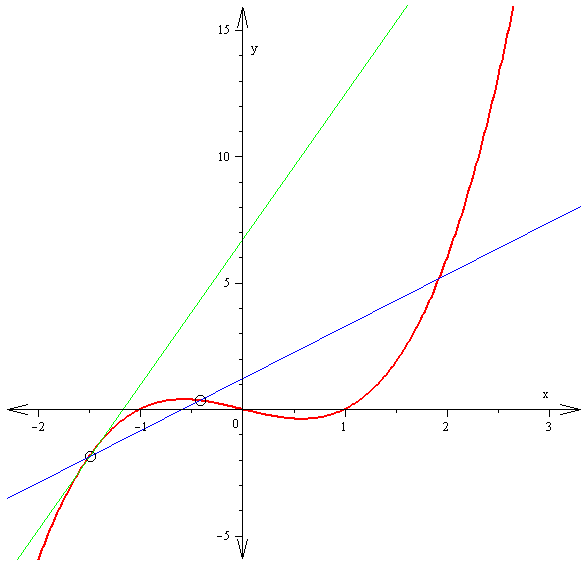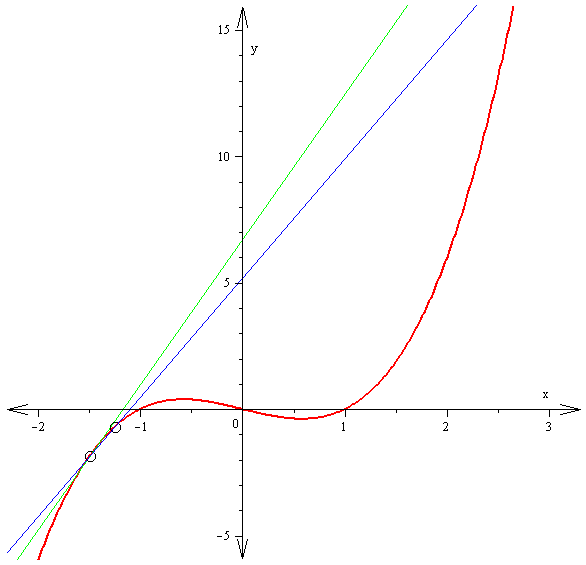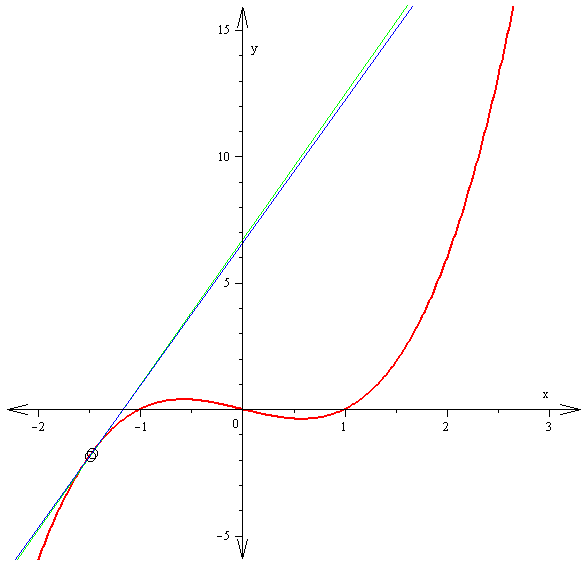
The derivative f′(x) of a curve at a point is the slope of the line tangent to that curve at that point.
This slope is determined by considering the limiting value of the slopes of secant lines.
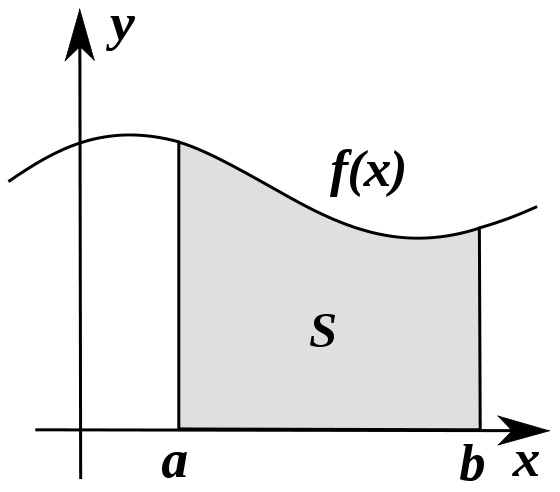
Integral calculus is about accumulation
Integration can be thought of as measuring the area under a curve, defined by f(x), between two points (here a and b).
Required readings
If you have never seen calculus, please read sections 2.2 and 2.4 from Wikipedia's article on the topic, but do not worry if you don't understand the algebraic details, i.e., just focus on gaining an intuition for rates and accumulation.Linear algebra
PageRank is matrix multiplication

Required videos
If you've never had linear algebra, please watch the first four videos in this series: the essence of linear algebra, and once again, don't worry so much about the details, but focus on gaining an intuition for the nature of the subject.Calculus vs. linear algebra
Probability and statistics
Required reading
If you've never had any probability and/or statistics, please read this post.Data science vs. statistics
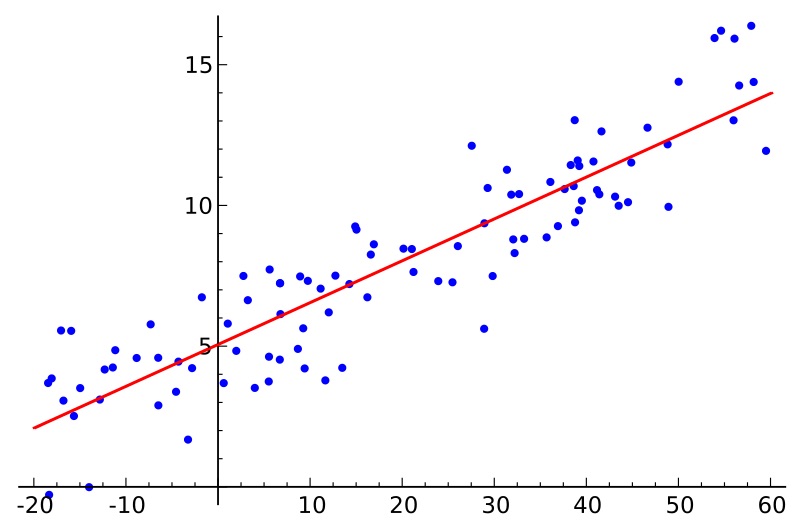
Regression
Objective functions
(and a grain of salt).
Hypothesis testing
p-values and hacking
Required reading: p-hacking

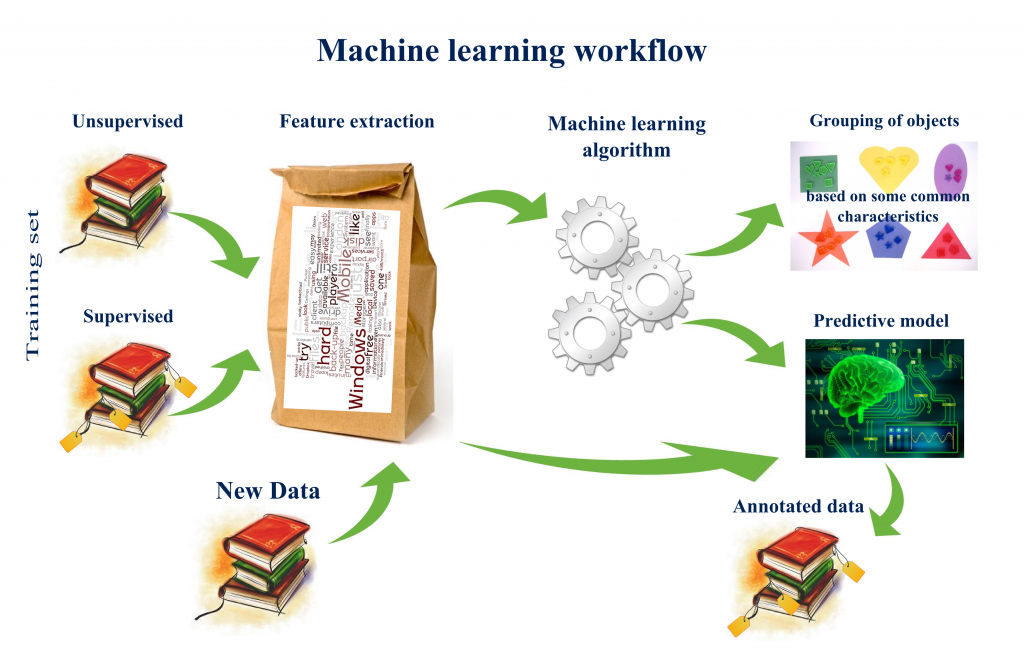
Machine learning
Required readings
1) A visual introduction to machine learning2) Statistics vs. machine learning
Model selection
- Some other selection factors:
- What model is a good theoretical match for the data?
- How efficiently or quickly does a model run?
- How domain-portable is a model?
- How difficult is a model to implement?
- Will the model scale across multiple machines?
- How transparent are a model's inner workings?
Required reading: DS model selection
The bias-variance tradeoff
- Modeling error can be broken down into three parts:
- bias error, due to the assumptions made in a model;
- variance error, due to sensitivity of a model on training;
- and irreducible error, due to factors unknown, often external.
Required reading: Bias-variance tradeoff
Are models necessary?
Required reading: The end of theory
Recap
- Next week: Classification
- How do machines discriminate?
- How is machine discrimination evaluated?
- What happens when machines make errors?